Fraktale wiederentdeckt – das Chaos Spiel

Es ist fast 30 Jahre her, dass ich mich mit dem Thema Fraktale intensiv auseinander gesetzt habe - damals Ende der 1980er Jahre war das ja auch ein richtiges Hype-Thema. Kürzlich habe ich das Thema noch mal aufbereitet und möchte hier noch mal kurz darüber berichten.

Ein kleines JAVA Programm, das die beschriebenen Algorithmen umsetzt und über eine kleine UI zugänglich macht, habe ich auf Github veröffentlicht.

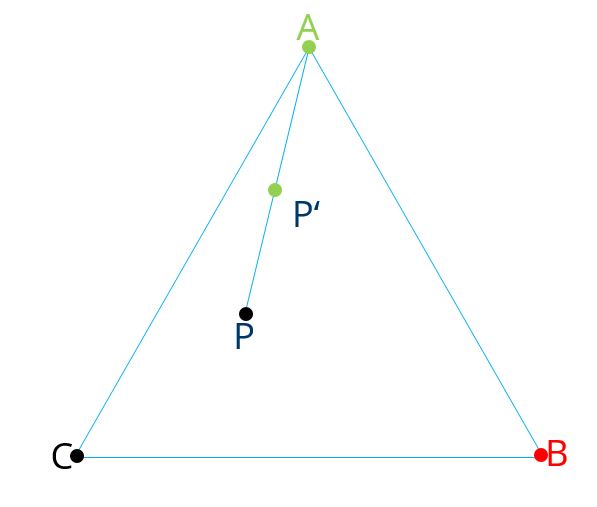
Eine interessante und amüsante Art, ein Fraktal zu erzeugen, ist das sogenannte "Chaos-Spiel" (vgl. "Fractal modelling of real world images" von M.F. Barnsley in "The Science of Fractal Images") . Dazu nehme man ein Blatt Papier und markiere darauf die Eckpunkte eines beliebig gearteten Dreieck und nenne sie A, B  und C. Dann wählt man einen beliebigen Punkt  P innerhalb des Dreiecks aus und markiert ihn. Mit einem Würfel wählt man eine der Ecken entsprechend der gewürfelten Augenzahl aus: A bei 1 oder 2, B bei 3 oder 4 und C bei 5 oder 6. In der Mitte der Verbindung zwischen P und dem Eckpunkt markiert man wiederum einen Punkt P'. Jetzt wird erneut gewürfelt und P'' ergibt sich in der Mitte der Verbindungslinie von P' zum Eckpunkt. Man wiederhole dieses Spiel einige tausend Male, um genügend Punkte zu erhalten.

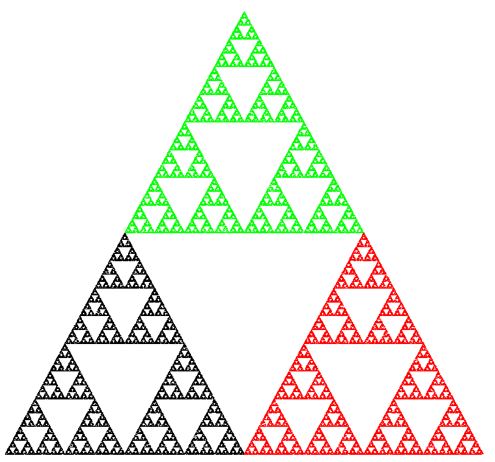
Eigentlich würde man erwarten, eine völlig chaotische Ansammlung von Punkten zu erhalten. Es ergibt sich jedoch ein regelmäßiges Muster, das sogenannte Sierpinski-Dreieck (nach dem polnischen Mathematiker Waclaw Sierpinski 1882-1969). Das nebenstehende Bild zweigt das entsprechende Fraktal.

Diese Spielregeln lassen sich relativ einfach mathematisch beschreiben: Einen neuen Punkt Pⁿ⁺¹ erhält man, indem man vom alten Punkt Pⁿ die halbe Weglänge zwischen Pⁿ und dem gewürfelten Eckpunkt E (also A, B, oder C) zurücklegt, also:

Pⁿ⁺¹ = Pⁿ + 1/2*(E-Pⁿ)  (vektoriell)

Oder in Matrixschreibweise und mit ausmultiplizierter Klammer und den Eckpunkten (0/0), (1/0) und (0,5/1):

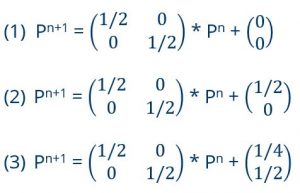
Diese Gleichungen stellen eine einfache lineare Transformation eines Punktes in der Ebene auf einen anderen Punkt der Ebene dar. Da zusätzliche zu den linearen Gewichten der Matrizen, mit denen der alte Punkt multipliziert wird, noch eine konstante Verschiebung hinzukommt, spricht mal von einer affin-linearen Transformation. Im allgemeinen können natürlich auch die Matrizen für jede Transformationsgleichung unterschiedlich sein.

Man kann das so interpretieren, dass die entstehende Figur (Menge), das Fraktal, ein Attraktor für die angegebenen Transformationen des Chaos-Spiels ist. Das heißt, dass man immer nach einer ausreichenden Anzahl von Iterationen auf einem Punkt dieser Figur landet, egal mit welchem Punkt man beginnt. Ist man einmal auf diesem Attraktor angelangt, kommt man von ihm nicht mehr los.

Die Darstellung mittels Transformationsgleichungen erweist sich als überaus vielseitig. Denn um andere (affin-lineare) Fraktale zu erzeugen, ändert sich an den Spielregeln nichts, nur der Inhalt der Matrizen und Vektoren und die Anzahl der Gleichungen variiert. Mit vier Transformationsgleichungen und anderen Werten ergibt sich zum Beispiel das Farnblatt rechts. Auch ein Ahornblatt oder die schon berühmte Kochkurve können so generiert werden. Die Beispiel sind in dem oben erwähnten Programm bereits eingebaut.

Mich hat Beschäftigung mit dem Thema Fraktale und Chaos Spiel wieder aufs neue fasziniert. In dem Programm sind noch einige andere implementiert, insbesondere ein "fraktaler Kopierer" ("Mehrfach-Verkleinerungs-Kopier-Maschine") , der auch sehr verblüffend ist. Doch dazu vielleicht später mal mehr in einem eigenen Artikel.